Les déterminants du taux d’épargne des ménages durant la crise du coronavirus.

La crise du coronavirus a eu de nombreux effets sur les indices macroéconomiques, l’un des plus notables concerne le taux d’épargne des ménages. En France, le taux d’épargne a augmenté de 1 % entre le quatrième trimestre de 2019 et le premier trimestre de 2020 passant de 14,6 % à 15,7 % d’après le tableau suivant. 

Figure 1 : Évolution du taux d’épargne des ménages en France entre 2019 et 2020

D’où provient cette hausse ? Le taux d’épargne se définit comme le pourcentage du revenu qui n’est pas consommé, en d’autres termes l’argent qui est mis de côté. La formule mathématique du taux d’épargne est comme suit, avec R représentant le revenu et C la consommation :

Un taux d’épargne qui est égal à 0 indique que le ménage consomme tout son revenu. En revanche, un taux d’épargne égal à 1 montre que le ménage épargne tout son revenu. Ainsi, si on s’arrête à cette première formule, le taux d’épargne est une formule qui dépend de deux variables : la consommation et le revenu. On peut expliquer l’élévation du taux d’épargne durant la crise du coronavirus par le fait que beaucoup de ménages ont subi durant cette période une baisse de leur revenu. La crise économique due au virus est à la fois une crise de l’offre et de la demande. Le confinement a contraint les ménages à ne plus consommer comme d’habitude. Des pans entiers de notre économie ont été touchés, par exemple la restauration a perdu 74 % de son chiffre d’affaires entre le 15 et 30 mars 2020 (1). Les entreprises ont dû faire face à une baisse de la demande. Nombre d’employés ont été contraints au chômage partiel ou pire ont été licenciés. Cependant, les aides mises en place par l’État ont permis à de nombreux ménages de garder à peu près les mêmes niveaux de salaires. Ainsi l’I.N.S.E.E. révèle qu’un quart des ménages pensent que leur situation financière s’est dégradée durant le premier confinement (2). Le salaire constitue pour la majorité des ménages la majeure partie de leur revenu. Ainsi la consommation a baissé du fait de la baisse de revenus. Les consommations moins essentielles (loisirs et culture par exemple) ont été revues à la baisse. Si le taux d’épargne a augmenté cela nous indique que la consommation a plus baissé que le revenu. Mathématiquement cela s’illustre comme suit :

Où R’ est le revenu du ménage durant la crise du coronavirus, C’ est la consommation du ménage durant le coronavirus, R est le revenu pré-COVID et C et la consommation pré-COVID.

Cette formule purement comptable ne permet pas à mon sens de rendre compte de toutes les variables qui affectent les ménages dans la formation du taux d’épargne. Pour essayer de comprendre à quoi est due cette hausse du taux d’épargne lors de la crise sanitaire, il faut prendre d’autres variables en compte. Le confinement a eu beaucoup d’effets sur la psychologie des individus. 

Ainsi dans cet article, nous allons proposer un modèle qui inclut divers théories et modèles économétriques pour mieux comprendre la hausse du taux d’épargne des ménages lors de la crise sanitaire.

La thèse classique sur l’épargne, le taux d’intérêt comme composante principale au taux d’épargne

La théorie néoclassique nous offre une porte d’entrée intéressante (quoi que simplificatrice) sur la détermination de l’offre d’épargne. Cette thèse se fonde principalement sur la notion de « préférence pour le présent ». Pour expliquer ce concept, nous allons faire une illustration mathématique. Tout d’abord, on définit une fonction d’utilité intertemporelle. Cette fonction permet de « quantifier » l’utilité que l’individu (donc le ménage) obtient en consommant un bien à deux périodes différentes. Mathématiquement cela s’écrit comme suit :

Où c₁ et c₂, sont respectivement les consommations à la date t = 1 et à la date t = 2 et β le facteur de préférence pour le présent. Imaginons que le ménage ait un taux de préférence pour le présent de 0. Alors qu’importe le nombre de consommation en t = 2, le ménage n’obtiendra aucune utilité de ces consommations. Ainsi, il préfère consommer tout à t = 1, ce qui nous permet d’affirmer que l’épargne de ce dit ménage est de 0.

Pour savoir combien un ménage épargne il faut que le profil intertemporel de consommation soit maximisé,  autrement dit, les différents revenus perçus à travers le temps actualisés du taux d’intérêt doivent maximiser l’utilité. Pour simplifier, nous supposons une économie comprenant deux dates (t = 1 et t = 2) et l’existence d’un marché financier intermédié, parfait et complet dont le taux d’intérêt nominal court est noté φ. Un marché financier dit “parfait et complet” est un marché financier permettant une allocation optimale des ressources. Il définit la rémunération additionnelle obtenue pour 1 €. Si l’agent place 1 € pendant 1 an, il recevra à terme (1 + φ) €. Le programme de l’agent s’énonce :

Où C₁ est le nombre de consommation du bien en t = 1, C₂ est la quantité du bien consommé en t=2, p₁ est le prix du bien en t = 1, p₂ est le prix du bien en t = 2, R₁ le revenu en t = 1, R₂ le revenu en t = 2,φ est le taux d’intérêt. La DBI est la droite de budget intertemporel. Cette droite exprime la richesse d’un consommateur en actualisant la valeur de tous ses revenus présents et futurs.

À l’équilibre, il n’existe aucune modification de consommation à chaque date qui permettrait d’augmenter l’utilité intemporelle de l’agent en respectant sa contrainte budgétaire consolidée. Cela se traduit par le fait que le taux d’intérêt psychologique est égal au taux d’intérêt réel. Avant d’aller plus loin, définissons ce qu’est le taux d’intérêt psychologique. Il mesure la quantité supplémentaire de bien à la date t = 2 qu’il faut donner au ménage pour qu’il renonce à consommer 1 unité de bien à la date t = 1 afin de conserver son utilité inchangée. À l’optimalité de la consommation, toute modification marginale de consommation temporelle rend invariante la satisfaction de l’agent.

Après manipulations mathématiques, il est possible de définir la quantité épargnée par un ménage comme une fonction à plusieurs variables :

Je laisse le lecteur averti lire la démonstration dans un manuel de micro-économie. Vous pouvez la trouver dans le livre Les agents en concurrence pure et parfaite de Franck Bien et Sophie Méritet.

Ainsi, on peut reformuler le taux d’épargne énoncé précédemment comme suit :

Maintenant, nous pouvons appliquer ce modèle à notre situation de départ à savoir la crise du coronavirus. Prenons un ménage quelconque où t =1 serait la période pré-covid et t = 2 la période pendant la crise sanitaire. Ce modèle économique donne une place prépondérante au taux d’intérêt réel. Imaginons que le taux d’intérêt en t=2 soit moins élevé que t=1 afin de relancer la machine économique. Cela signifie que le ménage à plus intérêt à consommer maintenant donc à emprunter. En effet, leur pouvoir d’achat sera moins conséquent en t=2.  

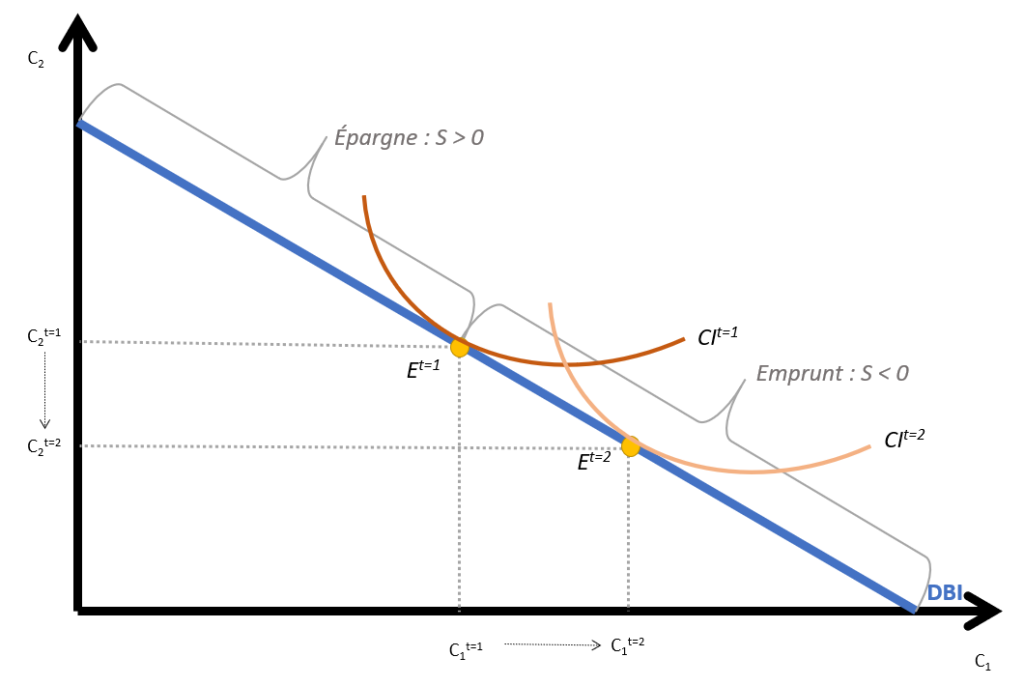
Ce graphique présente l’équilibre de consommation intertemporelle pour deux périodes. L’équilibre est atteint lorsque la courbe d’indifférence est tangente à droite de budget intertemporel. L’équilibre en t=1 (E^t=1) définit l’autarcie financière, c’est-à-dire que l’individu n’emprunte pas ni n’épargne. On sait qu’en t=2 le taux d’intérêt baisse pour favoriser la relance économique. Graphiquement, on assiste à une translation vers le bas de la courbe d’utilité, ici en orange. En effet, comme le taux d’intérêt a changé, la préférence pour le présent de l’individu a changé. Ainsi, on voit que le point d’équilibre en t= 2 (E^t=2) est « plus bas ». Cela se traduit par le fait que l’individu, au vu du faible taux d’intérêt, préfère consommer plus en t=1 et donc réduire sa consommation de bien en t=2 (C₂^t=2). Cette hausse de la consommation de bien en t=1 (C₁^t=1) se traduit par le fait que l’individu va devoir emprunter pour maximiser son utilité (sous hypothèse que la DBI reste constante).

Lors de la crise économique liée au coronavirus, les banques centrales ont décidé de baisser le taux directeur. Le taux directeur est le taux d’intérêt auquel la Banque Centrale prête des liquidités aux banques de second rang. Cette mesure doit inciter les entreprises et les ménages à investir (donc ne pas épargner) afin de relancer la machine économique. Par exemple, la Banque du Canada a fixé le taux directeur le 4 janvier 2020 à 1,75 % alors que le taux en septembre 2020 est de 0,25 %, comme on peut le voir sur le graphique suivant.

Figure 2 : Evolution du taux d’épargne au Canada entre 2019 et 2020

Si on suit cette logique, cette baisse du taux directeur aurait dû entraîner une baisse du taux d’épargne. Or cela n’est pas le cas, c’est même le contraire qui est observé. Le taux d’épargne des ménages était de 6,10 % lors du premier trimestre 2020, d’après le graphique suivant. Le second trimestre quant à lui voit le taux d’épargne des ménages bondir à 28, 2 %, soit une hausse de 22 points de pourcentage !

Figure 3 : Evolution du taux d’intérêt directeur de la Banque du Canada entre juillet 2017 et juillet 2020

Ainsi, nous pouvons voir que la hausse du taux d’épargne n’est pas liée aux taux d’intérêt. Il nous faut donc chercher d’autres raisons pour expliquer cette hausse.

Le rôle de l’inflation dans la fixation du taux d’épargne des ménages :

De prime abord, le lien entre l’inflation et le taux d’épargne peut effectivement être difficile à percevoir, pourtant ce lien existe bel et bien. L’inflation qui se définit comme la hausse des prix alors si l’inflation augmente alors le taux d’épargne baissera. Tout d’abord, l’inflation ruine l’épargne. Pour illustrer ce propos, on peut faire un tableau :

Somme épargnée à t = 1 (R)	Pourcentage de l’inflation entre t=1 et t=2	Niveau des prix en t=1 (P)	Pouvoir d’achat (R/P) en t=1	Pouvoir d’achat en t=2
500	0 %	1	500	500
500	100 %	1	500	250

Ce tableau permet d’illustrer le fait précédent. L’inflation réduit le pouvoir d’achat des encaisses réelles.  Dans la première situation, on s’aperçoit que même si dans les deux cas la somme épargnée est la même, le pouvoir d’achat en t = 2 est différent. On voit que si l’inflation est nulle alors le pouvoir d’achat de la somme épargnée reste le même. Dans le deuxième cas, les prix ont doublé ce qui entraîne une division par deux du pouvoir d’achat.

L’autre effet qui explique pourquoi le taux d’épargne est décroissant au taux d’inflation est le suivant : l’argent peut être moins épargné car la vie coûte plus chère. Par exemple, l’essence est une dépense non-négligeable pour un ménage. La hausse du prix augmentera la consommation du ménage et donc réduira son épargne. En effet, l’inflation entraîne une augmentation des prix. Ainsi, pour acheter le même bien, il faudra mettre plus d’argent afin de l’acquérir. Lors d’une inflation pure, c’est-à-dire lorsque les prix augmentent à « la même vitesse » que les salaires alors cela ne pose pas de problème. Dans la réalité, ce cas n’existe quasiment pas. Au contraire, les prix augmentent généralement plus rapidement que les salaires. Cela a pour effet d’appauvrir le salarié. A panier de consommation constant, il faudra consacrer une part plus importante du salaire à  la consommation. Ce qui réduit mécaniquement la propension à épargner. Cet effet est appelé « effet de revenu » ou « reconstitution de l’encaisse réelle ».

Après, ces deux affirmations, que nous disent les études empiriques ?

Premièrement, une étude menée au Pakistan “Microeconomics Determinants of Household Savings in Rural and Urban Areas: Evidence from Pakistan” (3) cherchant à comprendre les différences de comportements entre des ménages urbains et des ménages ruraux énonce que le taux d’inflation a un impact négatif sur le taux d’épargne. Ainsi les auteurs, décrivent la fonction d’épargne comme suit :

Où, SAV représente l’épargne des ménages, MI le revenu du ménage mensuel, DE l’éducation du ménage, DU si le ménage est urbain ou rural, DExDU l’interaction entre les deux variables. Les alphas sont des paramètres.

Cependant, cette affirmation est démentie dans un autre article de Philippe L’Hardy :  « Deux approches des comportements d’épargne des ménages » (4). Pour l’auteur, les ménages lors d’une période d’inflation se trouvent dans une situation ambiguë. Ils consomment et épargnent. Ainsi, il est difficile de cerner comment l’inflation impacte les choix des ménages. En période de hausse générale du niveau des prix, les ménages sont confrontés à deux choix. Le premier choix qui s’offre à eux est celui de la consommation. On appelle ce comportement « fuite devant la monnaie ». La monnaie devient une patate chaude dans les phases d’inflation. Ainsi, le ménage doit essayer de consommer pour utiliser au plus vite sa monnaie avant qu’elle ne perde trop de valeur, et qu’eux ne perdent trop de pouvoir d’achat. L’autre comportement concerne une augmentation de l’épargne, ce qui peut sembler contre-intuitif. Dans son article, l’auteur distingue le court terme et le long terme. Dans notre analyse, nous ne considérerons que le court terme pour des raisons évidentes. Pour l’auteur, lorsque le revenu augmente le taux d’épargne augmente. En effet, il semble difficile pour un ménage gagnant des millions d’euros par mois de consommer entièrement leur fortune. De plus, on peut vérifier empiriquement cette affirmation.

Figure 4 : L’évolution du taux d’épargne  en fonction du revenu brut disponible des ménages

Ce graphique montre  une corrélation nette entre la richesse d’un foyer et son taux d’épargne. En termes économiques, on dit alors que la propension marginale à consommer est décroissante par rapport au revenu. Mathématiquement cela s’écrit comme suit :

Où pmc, la propension marginale à consommer, ∂C/∂R est le rapport entre la variation de la consommation et la variation du revenu.

L’auteur constate dans son article que les variations du revenu réel sont très proches de celles des taux d’épargne. On peut représenter quantitativement cette relation par une équation de la forme suivante :

Où ARR est l’accroissement réel du revenu réel, a et b sont des paramètres de l’équation.

Ainsi les fluctuations du taux d’épargne dépendent de l’accroissement annuel du revenu des ménages. L’horizon temporel de ces fluctuations est de l’ordre d’un an. En un sens strict, il n’y a donc pas, à cet horizon temporel, d’effet direct de la hausse des prix sur le taux d’épargne : l’influence du niveau des prix est indirecte, elle ne se manifeste qu’à travers la variable « revenu réel », noté R/P. 

Figure 5 : Evolution de l’indice des prix à la consommation entre 2017 et 2020

Ainsi, comme le taux d’inflation a baissé en France durant l’année 2020, il était presque de 0 % en septembre 2020 – un record ! Si on suit la thèse précédente, les ménages sont devenus plus riches, si l’on considère le revenu constant. En effet, leurs revenus réels ont augmenté. En considérant que le pmc est décroissant, alors le taux d’épargne augmente mécaniquement. Cependant, comme dit dans l’introduction, les revenus des ménages ont baissé. Il nous faut donc chercher la réponse ailleurs

La théorie du cycle de vie :

Dans les années 1960, l’économiste Modigliani élabore une théorie visant à expliquer les cycles d’épargne et de désépargne de l’individu durant son existence. Cette théorie est fondée sur le fait que la consommation des individus reste stable dans le temps. Modigliani sépare la vie en trois périodes distinctes : T₁ symbolise la jeunesse, T₂ correspond à la période de la vie consacrée au travail rémunéré et T₃ représente la retraite. Lors de sa jeunesse, l’individu emprunte, par exemple pour ses  études. Lors de la deuxième période de sa vie, l’individu peut se permettre d’épargner car il ne consomme pas tout son revenu en consommation. Enfin, lors de sa fin de vie l’individu « grignote » ses économies afin de subvenir à ses besoins. Ce modèle permet d’expliquer en partie la façon dont  le taux d’épargne est fixé durant la crise du coronavirus. Durant l’épidémie certains individus ont pu penser que leur espérance de vie allait se réduire. En effet, plus de 1 million de personnes sont décédées de cette maladie (5). Ainsi, pour ces individus pensant que la fin serait plus proche, il faut plus épargner. Le temps est réduit, or s’ils veulent garder la même consommation (hypothèse de début) il leur faut plus épargner. T₁ ne changent pas car la proportion de jeunes (de 0 à 39 ans) qui meurent du virus est très faible, de l’ordre de 1 % de 0,56 % à partir des chiffres du 9 novembre en France (6). De plus, on peut supposer que T₃ est très peu élastique car chaque individu veut pouvoir profiter de ses vieux jours. La période T₂ est donc plus courte, et le taux d’épargne sera plus conséquent. On peut représenter cette situation graphiquement. A représente la période pré-crise et B représente la période durant la crise.

Que disent les faits ? Tout d’abord, il semble difficile d’infirmer cette théorie. Les choix de l’individu ont une logique de long-terme. Or, cela ne fait même pas un an que la crise sanitaire a débuté. Cependant, ce modèle à ses limites – comme tous les modèles. Premièrement, il serait illusoire de croire que les retraités n’épargnent pas. Le graphique ci-dessous montre que les plus de 70 ans ont un taux d’épargne avant transfert privés proche des 40-49 ans (respectivement 19,15 % pour les 70 ans et plus et 20,16 % pour les 40-49 ans). L’une des raisons principales à cela, est que les personnes âgées ont à cœur de transmettre une partie de leur patrimoine à leurs descendants.

Figure 6 : Taux d’épargne  en fonction de l’âge des ménages

Deuxièmement, comme dit précédemment, ce modèle est basé sur le modèle anglo-saxon. En France, les retraites sont financées par les cotisations et non pas par le capital construit durant toute la vie du salarié. Donc, ce modèle n’est pas forcément pertinent pour analyser la situation française.

Après avoir usé de thèses libérales, il est temps d’aller de l’autre côté de la force ; à savoir les keynésiens.

La thèse keynésienne :

Dans la théorie keynésienne, l’épargne est considérée comme un résidu de la consommation. Pour Keynes, il y a deux types de consommation. Premièrement, il y a la consommation incompressible. Cette consommation comprend tout ce que le ménage ne peut se soustraire à consommer sans mettre sa vie en péril. Si on veut le traduire en termes économiques, la consommation incompressible est l’ensemble des biens que les ménages consomment en ayant une élasticité-prix nulle. La demande de ces biens est très peu sensible à une variation du revenu ou des prix. Les exemples les plus équivoques sont la nourriture, le loyer ou la santé. Deuxièmement, on a la propension marginale à consommer qui est égale à la portion d’une hausse du revenu qui va vers la consommation. Si C₁ = 1 alors le ménage consomme tout son revenu.

 Si on admet, que l’épargne est la partie du revenu disponible brut non consommée alors, la fonction d’épargne keynésienne s’écrit comme suit : 

Où y est le revenu, C₀ la consommation incompressible, C₁ la propension marginale à consommer.

Nous pouvons réécrire notre taux d’épargne comme suit :

Ce modèle peut s’avérer pertinent pour élucider d’où vient cette hausse du taux d’épargne. Tout d’abord, nous savons que le revenu a baissé pour de nombreux ménages durant la crise sanitaire. Cependant, ce fait n’explique pas entièrement la hausse du taux d’épargne. En effet, si le revenu baisse mais que C₁ reste constante alors la consommation augmente, ce qui entraîne une baisse du taux d’épargne. Donc le deuxième effet qui explique cette hausse du taux d’épargne est une baisse de la propension marginale à consommer. Cette baisse peut trouver son explication par le fait que les ménages n’épargnent pas juste pour reporter de la consommation. Ils peuvent aussi faire de l’épargne de précaution. L’épargne de précaution est l’argent mis de côté en vue de se protéger de futurs coups-durs. Les ménages essaient d’anticiper la future situation économique. Si leurs prévisions ne sont pas bonnes comme par exemple lors d’une crise économique, les ménages auront moins confiance dans l’avenir et épargneront plus afin de mieux supporter les coups durs à venir. Graphiquement cette situation s’illustre comme suit :

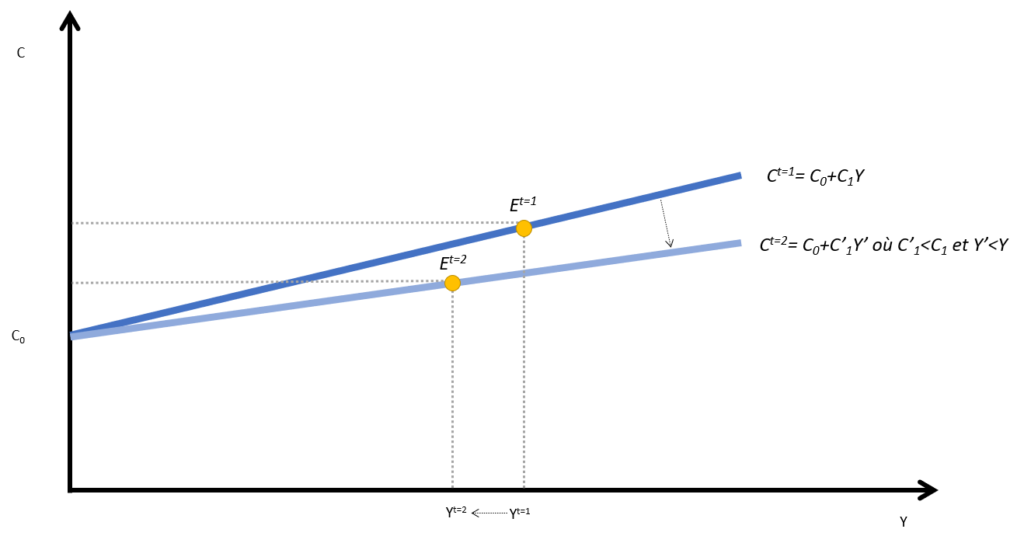
Tout d’abord, on peut voir que la courbe C^t=2 a « pivotée » vers le bas par rapport à la courbe C^t=1. En effet, C₁ est le coefficient directeur de la courbe donc quand il baisse, la courbe réduit sa pente. D’autre part, comme le revenu baisse alors le point d’équilibre en t=2 (E^t=2) se situera plus à gauche que le point d’équilibre en t=1 (E^t=1). Ce graphique montre bien la baisse de la consommation.          

Cette affirmation est-elle juste ? Grâce à une note de conjoncture de l’INSEE de septembre 2020 portant sur la consommation, on peut dire que la réalité vérifie bien ce modèle (5). Tout d’abord, nous pouvons affirmer que la demande pour les biens appartenant à la consommation incompressible n’a connu qu’une baisse minime. Le tableau ci-dessous montre bien cela. Tout d’abord, on constate que la demande pour les produits alimentaires a été stable, par exemple en août il n’y a eu aucun écart par rapport à la consommation avant la crise.  En revanche, la demande de produits moins essentiels à la survie a baissé de manière drastique. Par exemple, lors du 2^ème trimestre de 2020, l’hébergement et la restauration ont connu une baisse de 64 %. Enfin, on remarque que cette baisse de la consommation semble temporaire. Sur le long terme, on peut affirmer que la consommation retrouvera son niveau pré-covid. Si l’on regarde le total, on voit bien que la baisse de la consommation semble être de moins en moins importante. En effet, l’écart au 2^ème trimestre 2020 est de 17 % alors que l’écart en août 2020 n’est que de 2 %.

Figure 8 : Estimation de l’écart de niveau de consommation des ménages par rapport au niveau d’avant crise

On peut affirmer que cette baisse de la consommation est motivée par la hausse de l’épargne de précaution. Un sondage de l’IFOP nous révèle ainsi que le coronavirus inquiète les personnes tant sur le plan personnel qu’économique. Ainsi, l’évolution de la proportion de personnes inquiètes du coronavirus à l’égard des conséquences économiques de la crise est caractérisée par sa stabilité et son haut taux (> 85 %), comme on peut le voir sur le graphique suivant.

Figure 10

Construction d’un modèle où la confiance est supposé être le principal déterminant du taux d’épargne

Ainsi, il est utile de comprendre comment les chocs de confiance impactent le taux d’épargne. Pour cela, je propose un modèle qui fixe comme déterminant principal la confiance dans l’économie, l’élément clé du taux d’épargne. Ce modèle peut nous permettre de mieux comprendre comment les chocs de confiance affectent le taux d’épargne.

Dans ce modèle, on suppose que le ménage définit son taux d’épargne en deux temps. Tout d’abord, le ménage fixe un taux d’épargne qui omet la confiance dans l’économie. Dans un deuxième temps, le ménage incorpore la confiance dans la détermination de son taux d’épargne.

On peut traduire ce modèle via une formule mathématiques :

Où τ_e est le taux d’épargne qui omet le facteur « confiance des ménages dans l’avenir », α est le coefficient qui traduit le facteur « confiance des ménages dans l’avenir » et τ^’_e exprime le taux d’épargne qui prends en compte le facteur « confiance es ménages dans l’avenir ».

De plus, on peut déterminer le maximum que peut prendre α.

On sait que :

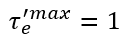
En effet, l’individu ne peut pas épargner plus que son revenu. Dès lors :

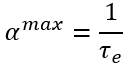
Du fait de la limite du taux d’épargne, α ne peut avoir un effet infini sur le taux d’épargne. A partir d’un certain seuil (α^max), une hausse du pessimisme des ménages n’entraîne pas une hausse du taux d’épargne car celui-ci est déjà à son maximum – en supposant que le taux d’épargne qui omet α reste constant. On peut supposer que le pessimisme des ménages est infini alors que le taux d’épargne est soumis à un seuil. Ainsi, pour une hausse de α dépassant α^max, les ménages ne pourront pas répercuter leur pessimisme dans une hausse du taux d’épargne car celui-ci est déjà égal à 1.

Pour comprendre comment α influence 𝜏^’_e, on peut faire un tableau résumant tous les cas possibles.

Ainsi, α joue tantôt un rôle d’accélérateur ou un rôle de ralentissement dans la formation du taux d’épargne. Maintenant, il nous faut comprendre l’élasticité entre ces deux variables. En effet, il est utile ici d’adopter un raisonnement marginaliste. Ce genre de raisonnement conduit à étudier la variation de la dernière unité. Pour cela, nous ferons l’hypothèse que τ_e est constant. La formule alors du taux d’épargne se réécrit :

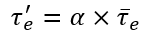
En faisant cela, on étudie alors plus que les variation τ’_e en fonction de α. Cela simplifie l’analyse. Ainsi, nous pouvons esquisser trois cas. Le premier concerne une situation dans laquelle l’accroissement de α entraîne une hausse de plus en plus rapide τ’_e. Le deuxi-me cas est l’invers de la première situation. C’est-à-dire, quand α augmente, τ’_e augmente de moins en moins vite. La dernière situation traduit une hausse linéaire de τ’_e quand α croît. Graphiquement, cela s’illustre comme suit :

Cependant, laquelle de ces trois courbes représente le mieux la réalité ? Pour cela, il nous faut calculer l’élasticité entre le taux d’épargne et la confiance. Cela nous permettra de comprendre comment évolue le taux d’épargne en fonction de la confiance des ménages. Nous calculerons trois élasticités à trois périodes différentes. La variable qui représentera la confiance sera l’indicateur « la confiance des ménages », calculée chaque mois. Cet indice est calculé via un formulaire constitué de plusieurs questions rempli par différents ménages rédigé par l’I.N.S.E.E. La première période 2019-2018, illustre un moment où le taux d’épargne était à un taux « normal » (~15 %). La deuxième période 1989-1988 quant à elle se situe à un moment où les taux d’épargne étaient faibles (~11 %). Enfin, la troisième période 1978-1977 est marquée par des taux d’épargne élevés (~20 %). Pour calculer l’élasticité du taux d’épargne à la confiance, on utilise la formule suivante :

On peut dès lors affirmer, que plus le taux d’épargne est haut, plus il est sensible à une variation de la confiance. En d’autres termes, plus le taux d’épargne est élevé, plus la confiance joue un rôle déterminant. La courbe qui vérifie le mieux ce cas de figure est la courbe bleue du graphique précédent. Dès lors, il est plus aisé de comprendre comment les chocs de confiance impactent le taux d’épargne. Ce modèle peut ainsi nous éclairer sur la crise du coronavirus. A l’heure où cet article est rédigé, la France est à son deuxième confinement. Ainsi, on peut essayer de prédire comment va réagir le taux d’épargne à ce nouveau confinement. On peut s’attendre à ce que la hausse du taux d’épargne soit encore plus forte que durant le premier confinement. En effet, les ménages ont connu deux chocs de confiance négatifs, le premier et le deuxième confinement. Cette situation s’illustre graphiquement comme suit :

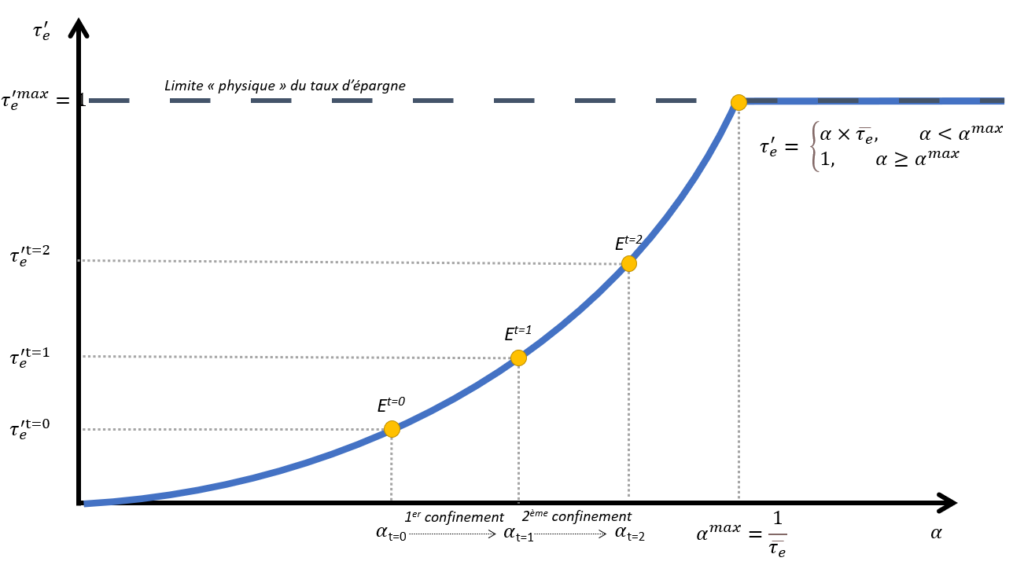
Ainsi, on peut déduire que la hausse du taux d’épargne des ménages lors du deuxième confinement sera plus importante que durant le premier confinement.

En conclusion, il serait illusoire de croire que l’évolution du taux d’épargne n’est due qu’à un seul déterminant. Durant les crises économiques, il peut être difficile de prédire et de comprendre l’évolution des indicateurs macroéconomiques. Ces évènements impactent en profondeur les mentalités et les vies des personnes. Il serait tautologique de résumer entièrement les choix des ménages via le recours à des modèles économiques. Il est évident qu’il existe des déterminants bien plus complexes et difficiles à traduire mathématiquement. L’épargne n’est pas juste de la consommation différée ou une traduction de la confiance des ménages. Il peut être source de prestige social, d’héritage par exemple. Enfin, le taux d’épargne est un élément clé de la compréhension de notre économie. Il est le principal facteur permettant l’accumulation de capital au sein de l’économie. Ainsi, le taux d’épargne des ménages influent indirectement sur la croissance.

Sources : 

(1) Maddyness. 17/03/2020. “L’effet domino de la crise sur le secteur du food service”. Accessible à:https://www.maddyness.com/2020/04/17/infographie-food-service-coronavirus/  [08/11/2020].(2) I.N.S.E.E. 14/10/2020 “ Confinement : des conséquences économiques inégales selon les ménages”. Accessible à : https://www.insee.fr/fr/statistiques/4801313 [08/10/2020]

(2) I.N.S.E.E. 06/10/2020. “Point de conjecture du 8 septembre”. Accessible à : https://www.insee.fr/fr/statistiques/4653862?sommaire=4473296 [10/11/2020]

(3) Iqbal, Hui, Khurshaid et Hafeez. Juillet 2018. “Microeconomics Determinants of Household Savings in Rural and Urban Areas: Evidence from Pakistan”. 

(4) L’Hardy, P. 1975. “L’épargnant dans l’inflation”. Economie et Statistiques. Numéro 66, pages 39-43

(5) Johns Hopkins University . “COVID-19 Dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU)”. Accessible à: https://gisanddata.maps.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6 [10/11/2020]

(6) Franceinfo. “INFOGRAPHIES. Coronavirus : morts, hospitalisations, âge des malades… Suivez l’évolution de l’épidémie en France et dans le monde”. Accessible à : https://www.francetvinfo.fr/sante/maladie/coronavirus/infographies-covid-19-morts-hospitalisations-age-malades-l-evolution-de-l-epidemie-en-france-et-dans-le-monde-en-cartes-et-graphiques.html [10/11/2020]

Sources figure :

1. Banque de France. 14/08/2020. “Epargne des ménages 2020T1”. Accessible à : https://www.banque-france.fr/statistiques/epargne-et-comptes-nationaux-financiers/epargne-des-menages [10/11/2020]
2. Banque du Canada.”Taux directeur”. Accessible à :  https://www.banqueducanada.ca/grandes-fonctions/politique-monetaire/taux-directeur/ [10/11/2020]
3. Tradingeconomics. “Canada Household Saving Rate”. Accessible à : https://tradingeconomics.com/canada/personal-savings [10/11/2020]
4. I.N.S.E.E. 30/05/2017. “Les comptes de la Nation en 2016”. Accessible à : https://www.insee.fr/fr/statistiques/3148891?sommaire=2832834 [10/11/2020]
5. I.N.S.E.E. 30/09/2020. “En septembre 2020, les prix à la consommation augmentent de 0,1 % sur un an”. Accessible à : https://www.insee.fr/fr/statistiques/4770780 [10/11/2020]
6. I.N.S.E.E. 30/05/2017. “Les comptes de la Nation en 2016”. Accessible à : https://www.insee.fr/fr/statistiques/3148891?sommaire=2832834 [10/11/2020]
7. I.N.S.E.E. 06/10/2020. “Point de conjecture de 2020”. Accessible à :https://www.insee.fr/fr/statistiques/4653862?sommaire=4473296 [10/11/2020
8. I.F.O.P. “Les français et l’épidémie de COVID-19”. Accessible à : https://www.ifop.com/publication/les-francais-et-lepidemie-de-covid-19-2/ [10/11/2020]