
Il peut être difficile pour le citoyen lambda de réellement comprendre la portée et la raison des politiques économiques menées. Cette série d’articles présente un des modèles les plus connus en économie : IS-LM. Dans les prochains “épisodes” nous appliquerons le modèle au plan de relance français pour faire face au covid-19 puis nous étudierons les grandes variations de ce modèles. IS-LM a été théorisé dans les années 30 par John Hicks (1) et a pour objet de formaliser mathématiquement certaines idées keynésiennes, tout en intégrant des idées néoclassiques. C’est pourquoi, IS-LM est un des fondements du courant de pensée appelé la synthèse néoclassique. Cependant, comme tout modèle, il est fondé sur des axiomes qui sont des représentations simplifiées de la réalité. Par conséquent, il faut toujours garder à l’esprit les limites du modèle présenté ici et ne pas le prendre comme parole d’évangile.
Ce modèle permet d’expliquer – grossièrement – comment les politiques budgétaires et monétaires affectent les grands indicateurs macro-économiques dans un contexte de chômage structurel.
Présentation du modèle en économie fermée :
Le système part de deux courbes fondamentales. À savoir la courbe IS et la courbe LM. Tout d’abord, expliquons à quoi correspond cette fameuse courbe IS.
La courbe IS est l’ensemble des couples qui vérifient l’équilibre entre le taux d’intérêt (R) et le niveau de production – qui sera mesuré par le P.I.B. (noté Y) – sur le marché des biens.
La formule correspondante à cette courbe est la suivante en économie fermée :
D’autre part, nous affirmons que l’investissement dépend de la confiance des entreprises dans l’avenir (perspective de profits) et du taux d’intérêt (coût de l’investissement). On peut réécrire la fonction de l’investissement comme suit :
Cette courbe est décroissante dans le plan (Y,R). En effet, lorsque le taux d’intérêt augmente, la consommation diminue parce que la propension à épargner augmente. Puisque l’épargne est plus rémunératrice, les ménages – qui déterminent le niveau de consommation – ont moins intérêt à consommer. D’autre part, le taux d’intérêt (R) affecte négativement l’investissement. Le taux d’intérêt (R) représente le coût de l’emprunt. Or si R augmente, l’investissement par l’emprunt coûte plus cher. Enfin, la dépense publique (G) décroît lorsque R augmente. La même logique que l’investissement privé (I) s’applique. La plupart du temps, la dépense publique est financée par l’emprunt. Si une des composantes (C,I et G) de la courbe IS est amenée à varier alors la courbe se déplace dans le plan. Imaginons que G diminue alors la courbe IS va subir un choc négatif, ce qui fait translater la courbe IS vers la gauche.
Après avoir présenté IS, on peut maintenant présenter la courbe LM. Celle-ci se définit comme l’ensemble des situations, des couples, (Y,R), qui vérifient l’équilibre sur le marché de la monnaie. C’est-à-dire que l’offre de monnaie est égale à la demande de monnaie. Sa formule mathématique s’énonce comme suit :
On peut réécrire, M^d/P, comme suit :
Expliquons à quoi correspond l(Y,R) : l représente la fonction de préférence pour la liquidité. Elle dépend de deux variables à savoir R et Y. Les ménages demandent de la monnaie pour deux raisons. Tout d’abord, il y a un impératif de facilité des transactions, les ménages ayant besoin de liquidités pour effectuer leurs achats. D’autre part, il y a un motif de spéculation au regard des titres que les ménages détiennent. Or quand R diminue, les ménages sont incités à détenir plus de liquidités car l’épargne est moins rémunératrice. Si une des composantes (M^d/P ou M^s/P) de la courbe LM est amenée à varier alors la courbe se déplace dans le plan. Imaginons que M^s/P diminue alors la courbe LM va subir un choc négatif, ce qui fait translater la courbe LM vers la gauche.
Le croisement des courbes LM et IS dans le plan (Y,R) permet de déterminer l’équilibre de l’économie, c’est-à-dire le point d’équilibre entre la production Y* et le taux d’intérêt R* assurant l’équilibre. Graphiquement cela s’illustre comme suit :
Présentation du marché du travail :
Après s’être intéressé au marché de la monnaie et des biens, on peut maintenant évoquer le marché du travail. Ce marché est caractérisé par une demande – ici les entreprises – et une offre, constituée de la population active. La population active, au sens du Bureau International du Travail (BIT), est la somme de l’emploi et du chômage. Ici, nous considérerons que l’offre de travail – c’est-à-dire la quantité que les individus sont prêts à offrir – est fixe. Le graphique ci-dessous montre qu’à court terme, la population active varie très peu, et même qu’elle à tendance à se stabiliser dans le temps.
D’autre part, nous supposerons que la France se trouve dans une situation de chômage structurel. Pour certains économistes, ce chômage structurel proviendrait de l’existence d’un salaire réel (W/P) fixé au-dessus du niveau de salaire qui permettrait d’assurer le plein emploi. Le plein emploi est atteint lorsque les entreprises embauchent l’ensemble de la population active. Pour simplifier l’analyse, nous supposerons qu’il n’existe qu’une entreprise. Nous pouvons ainsi, représenter le marché du travail par un graphique:
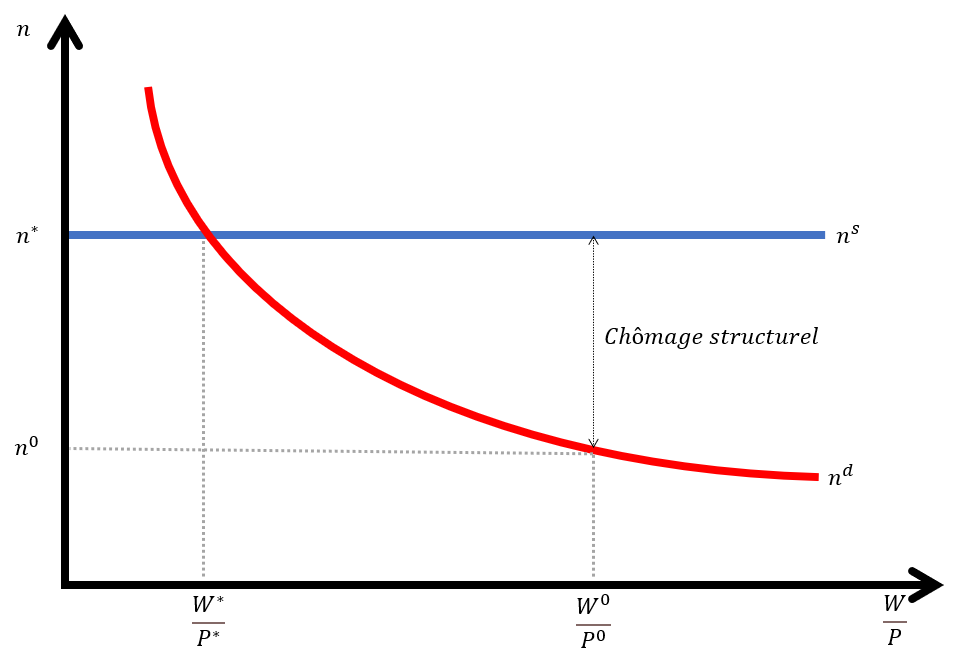
D’autre part, comme pour la fonction d’investissement, on intègre un paramètre symbolisant la confiance des entreprises dans l’avenir. Ainsi, on peut écrire la fonction de demande de travail comme suit :
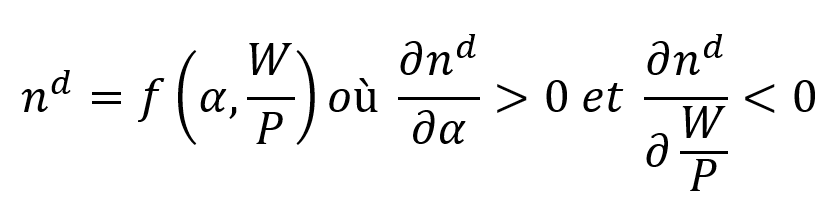
Présentation de la contrainte technologique de la firme :
Nous conservons l’hypothèse selon laquelle il n’existe qu’une seule firme. L’entreprise est contrainte par la quantité de travail et de son niveau de productivité pour produire les biens. De plus, on fera l’hypothèse que la productivité (a) dépend de deux variables: l’investissement privé (I) et la dépense publique (G). C’est-à-dire que la productivité de l’entreprise augmente lorsque le décideur public ou l’entreprise investissent. Par exemple, investir dans des nouvelles machines ou dans l’amélioration des infrastructures permet de produire plus, tout en gardant le même niveau d’emploi. La formule de la productivité s’écrit comme suit :
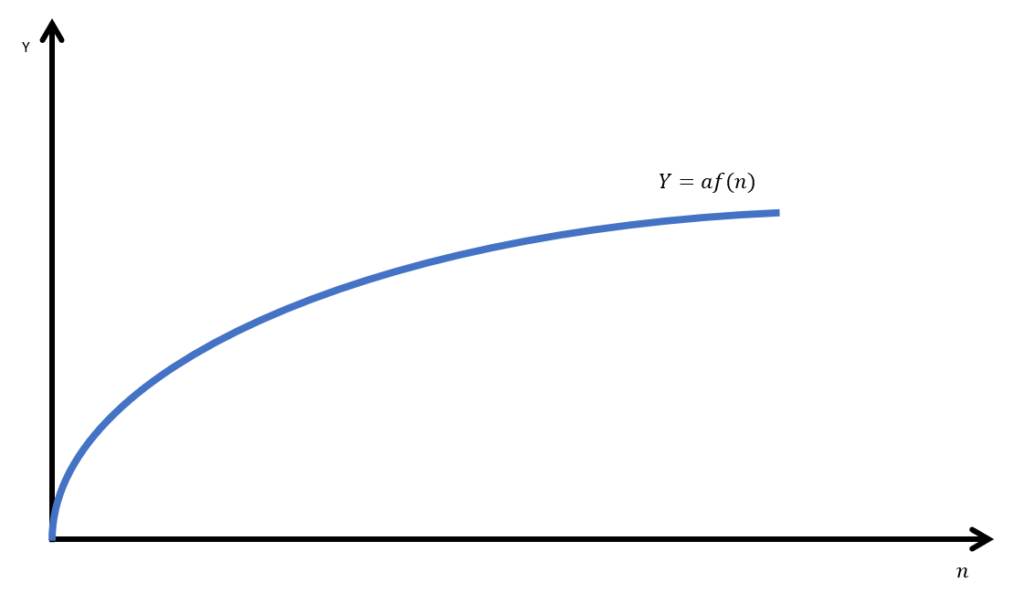
De plus, nous ferons l’hypothèse que le facteur de production – à savoir ici les employés (n) – possède une productivité marginale décroissante. C’est-à-dire que la dernière personne embauchée est moins productive que la précédente. Cette productivité marginale décroissante du travail peut être représentée par un graphique :
En conclusion, le modèle IS-LM en économie fermée est une bonne porte d’entrée pour comprendre les mécanismes liés à l’action gouvernementale. Cependant, le modèle IS-LM souffre de plusieurs lacunes. Tout d’abord, le modèle IS-LM fonctionne à prix fixe et à court-terme. Cela ne permet pas une analyse très poussée des chocs. De plus, il existe un débat sur la courbe LM. En effet, dans ce modèle, l’offre de monnaie est exogène. Cette conception de la monnaie est très débattue dans la science économique et certains économistes suggèrent que l’offre de monnaie est endogène. Dans cet article, j’ai fait le choix de réduire et de simplifier grandement le modèle pour permettre de vulgariser au mieux ce modèle. De plus, j’ai effectué quelques changements au modèle de base, notamment à travers l’ajout de variables symbolisant la confiance.
Sources :
- Hicks, J. 1937. “Mr. Keynes and the “Classics”; A Suggested Interpretation”. Econometrica. Volume 5, Numéro 2, Pages 147-159
- INSEE. 23/06/2020. “Activité, emploi et chômage en 2019 et en séries longues”. Accessible à : https://www.insee.fr/fr/statistiques/4498649?sommaire=4498692 [23/02/2021]






