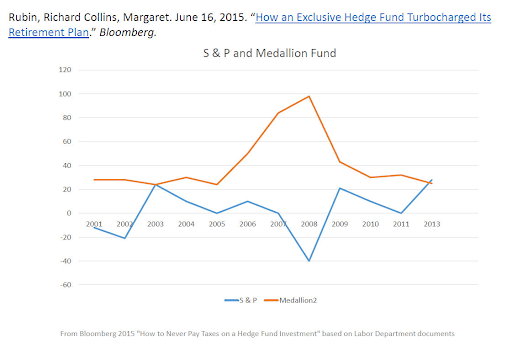
Le modèle de marche aléatoire est la première tentative de description du comportement stochastique des prix sur les marchés financiers. Il suit la théorie de Bachelier qui a conduit aux concepts de l’analyse moderne (martingale, mesures neutres au risque, ..), mais présente bien sûr quelques faiblesses. Aujourd’hui, l’accent sur la bonne modélisation mathématique de l’évolution des valeurs d’instruments financiers est la clé pour investir de manière efficace. Renaissance Technologies et son portefeuille le plus rentable et célèbre (Medallion Fund) est l’exemple même sur lequel chaque quant prête attention. Les modèles mathématiques utilisés par ce fonds sont extrêmement complexes et innovants. De 2001 à 2013, la pire performance annuelle du fonds a été de 21% (post déduction des frais). Si en 2008 l’indice Standard & Poor’s 500 avait perdu 38,5%, Medallion avait au contraire enregistré un gain de 98,2%.
L’oeuvre pionnière La théorie de la spéculation de 1900 de Louis Jean Baptiste Bachelier fut le point de départ de la finance moderne. Après avoir étudié un phénomène physique bien connu, le mouvement brownien, le mathématicien français a eu l’ingéniosité de l’appliquer comme modèle pour analyser l’évolution des prix sur les marchés boursiers.
Description du mouvement brownien
Bachelier avait pour objectif d’essayer de développer des formules mathématiques afin de déterminer le prix d’instruments dérivés complexes. Pour ce faire, comprendre la variation des cours des actions à la base de ces instruments était indispensable. Rapidement, le mathématicien comprend que :
“La détermination de ces activités dépend d’un nombre infini de facteurs: on ne peut donc absolument pas espérer pouvoir formuler une prévision mathématique (exacte)”.
Louis Bachelier
L’idée fondamentale de Bachelier pour estimer la probabilité de changement des prix est de considérer le marché obligataire comme un jeu équilibré. Pour comprendre ce concept, vous pouvez imaginer un jeu de pile et face entre deux joueurs. Pour N lancés, lorsque pile apparaît, le joueur gagne 1 euro, et vice versa, lorsque face apparaît, il perd 1 euro. À chaque lancer, pile et face ont la même chance de se présenter. Chaque lancer est donc indépendant du précédent, c’est-à-dire que le premier lancer n’a pas d’implications sur le deuxième.
En clair, l’idée principale de Bachelier est que l’argent, d’un point de vue probabiliste, après une longue série de lancements, devrait apporter un profit nul.
Marche aléatoire
Dans l’expérience du jeu équilibré avec une pièce lancée N fois, le résultat est suivi (+ 1, -1) pour chaque lancer. Cet exemple se réfère àce que l’on appelle en mathématiques un processus stochastique ou aléatoire, également appelé marche aléatoire.
Ce terme a été introduit pour la première fois en 1905 par le statisticien Karl Pearson, qui a illustré le problème en utilisant la métaphore de l’homme ivre, marchant et chancelant dans un champ ouvert. L’homme, titubant pendant son voyage fera quelques pas dans un sens, puis dans un autre et ainsi de suite. Après un moment, si vous voulez chercher l’homme ivre où devez-vous chercher? L’endroit le plus probable pour retrouver l’homme ivre se trouve juste à côté de son point de départ.
Comme pile ou face, cette expérience peut décrire le chemin aléatoire d’une particule qui peut se déplacer dans n’importe quelle direction avec la même probabilité. De même, ce processus peut également décrire les fluctuations du cours de l’action, qui effectue une série de mouvements aléatoires. Le prix peut monter ou descendre mais en moyenne il fluctue autour du point de départ. Bachelier est ainsi parti de cette conclusion pour construire son modèle.
Selon son modèle, la variation des prix ne peut être attribuée à aucune corrélation séquentielle, mais au contraire, elle doit être considérée comme aléatoire. Par conséquent, selon sa théorie, la tendance passée des prix ne peut pas être un indicateur fiable pour prédire la direction des fluctuations à l’avenir.
Cette théorie se fonde sur l’hypothèse d’efficacité du marché, c’est-à-dire qu’il suppose une grande transparence de l’actualité financière des entreprises, devenant accessible à la plupart des investisseurs. Selon cette hypothèse, le prix actuel d’une entreprise représenterait alors une bonne estimation de sa valeur intrinsèque et toute différence entre ces deux paramètres doit être imputée exclusivement aux informations en lien avec le titre lui-même. Ces facteurs alternant de manière irrégulière, il s’ensuit que les prix décrivent également une succession de données irrégulières et indépendantes. En fin de compte, la théorie Random Walk nie l’existence de la tendance et considère toute prédiction basée sur des modèles statistiques-mathématiques ou sur l’observation de graphiques comme peu fiable.
Limites de la pensée de Bachelier
La théorie révolutionnaire de Bachelier n’est toutefois pas sans limites. En utilisant la marche aléatoire pour décrire la trajectoire de prix d’un titre, il est possible, par nature même du processus, qu’il dépasse le seuil zéro, générant ainsi des nombres négatifs, i.e des prix négatifs, ce qui, dans la réalité ne peut se produire.
Après que l’économiste Paul Samuelson ait, en 1960, redécouvert le travail du mathématicien français, la théorie de Bachelier a été revisitée en supposant que ce n’est pas tant la variation du prix qui affecte, mais la variation proportionnelle du prix. Ce problème, peut être mathématiquement géré avec le logarithme.
De plus, du fait que les prix ne bougent pas d’une unité, une autre différence entre le modèle Bachelier et la finance réelle est que les marchés évoluent continuellement. Le temps s’étend sur toute la ligne des nombres réels positifs, et non en temps discret où il prend plutôt de la valeur dans l’ensemble des nombres naturels (t = 0, 1, 2, 3, etc.), comme dans l’exemple de pile ou face. À cet égard, Bachelier a conçu une théorie importante pour la transition du discret au continu, malheureusement manquant de rigueur en raison de l’absence d’outils mathématiques nécessaires.
Le point de vue mathématique
En 1923, Norbert Wiener a produit une construction mathématique rigoureuse de la théorie de Bachelier, directement en temps continu, basée sur le processus du mouvement brownien. Mathématiquement, un mouvement brownien est décrit par ce qu’on appelle le processus de Wiener, qui est un processus stochastique indexé par le temps continu. Pour la simplicité du traitement, nous considérons comme l’instant initial t = 0.
Le mouvement brownien a certaines propriétés pertinentes. Les incréments décrits dans le processus de Wiener, par exemple, sont indépendants et sont normalement distribués. La distribution de probabilité, en statistique, est une fonction qui montre les valeurs possibles pour une variable et la fréquence à laquelle elles se produisent.
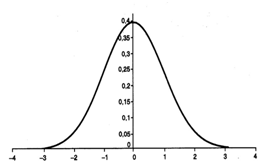
La distribution la plus connue et la plus utilisée est précisément la distribution normale, exprimée par la courbe de Gauss et utilisée pour expliquer de nombreux phénomènes naturels et économiques. Si les valeurs suivent cette courbe, qui prend la forme d’une cloche, dans la pratique, vous ne trouverez presque jamais un cas qui s’écarte beaucoup de la moyenne. Cette distribution de probabilité peut décrire des variables telles que la taille d’une population, les résultats du test de QI ou, pour revenir à Bachelier, les gains en jouant à pile ou face.
Comme l’a deviné Bachelier, si toutes les variations de prix d’une obligation relatives à une certaine période de temps sont organisées dans un diagramme, elles sont organisées sous la forme habituelle d’une courbe en cloche.
Précurseur d’idées révolutionnaires
En 1965, le doctorant de l’Université de Chicago Eugene Fama s’inspire des analyses de Bachelier et formule l’hypothèse dite des marchés efficients, fournissant ainsi la base sur laquelle repose la théorie financière moderne. Selon Bachelier, les fluctuations de prix ont été principalement causées par des facteurs irrationnels, qui s’annulent globalement symétriquement, générant des attentes de profit nul. Au contraire, Fama a attribué le caractère aléatoire à des marchés efficaces, dans lesquels la concurrence entre des participants complètement rationnels conduit à une situation dans laquelle les prix des titres individuels reflètent déjà les effets des informations sur les événements qui se sont produits et devront se produire.
Dans un marché efficace, à tout moment, le prix réel du titre sera une estimation de sa valeur intrinsèque. La version de Fama ne diffère pas du résultat de la marche aléatoire de Bachelier mais en déduit une caractéristique plus convaincante : les marchés sont impossibles à prévoir non pas parce qu’ils sont irrationnels mais parce qu’ils incorporent déjà toutes les informations disponibles. Ce modèle part de la constatation d’une linéarité imparfaite entre le rendement et le risque, mesuré par le bêta, et est basé sur l’approche multifactorielle. En particulier, ce modèle ajoute deux indicateurs de risques fondamentaux au coefficient bêta du CAPM : la taille de l’entreprise et l’inverse des multiples P/BV (Price / Book Value).
Bien qu’il puisse exister une relation inverse entre la taille, mesurée par la valeur de marché ou la capitalisation boursière, et les rendements des actions, cette tendance ne s’accompagne pas d’une augmentation (ou d’une diminution) du bêta. En règle générale, les titres d’une grande entreprise devraient être moins risqués et donc moins rentables. En revanche, les titres de petites sociétés devraient calculer un risque et un rendement plus élevés. Cela inciterait l’investisseur à demander une prime plus élevée pour compenser le risque supplémentaire.
La relation entre la valeur comptable et la valeur de marché a également un fort pouvoir explicatif : une valeur élevée du ratio (P / BV faible) distingue les titres à faible croissance et donc moins risqués ; les titres qui présentent une faible valeur de l’indicateur en question (P / BV élevé) dénotent de bonnes perspectives de croissance et des actifs incorporels élevés qui se reflètent dans la valeur de marché plutôt que dans la valeur comptable.
Pour ces deux cas (taille et valeur comptable par rapport au marché), Fama et French constatent que les preuves empiriques sont très différentes de l’énoncé théorique et que les primes de risque ne dépendent pas uniquement du risque systématique, mesuré par le bêta, mais au contraire, ils montrent une plus grande sensibilité à l’égard de la performance des trois facteurs considérés ensemble.
Renaissance Technologies, le hedge fund des scientifiques
Renaissance Technologies est le célèbre hedge fund qui enregistre des performances record depuis les années 1980. Renaissance est considéré par beaucoup comme “la plus grosse machine à argent de l’histoire de la finance”, puisque son principal fonds, Medallion, a gagné en moyenne 40% par an depuis sa création, déjà net de frais : un rendement incroyable même pour un fonds de couverture. Pour faire une comparaison, il suffit de penser que dans la même période, l’indice Standard & Poor’s 500 (S&P500) a gagné 10% et Warren Buffett détenant Berkshire Hathaway seulement 16%.
Se pose alors la question de ce qui différencie ce fonds de tous les autres et ce qui le rend si performant. La réponse est que le succès de ce fonds est essentiellement dû à l’esprit brillant de son fondateur, James Simons, un mathématicien de renommée mondiale.
Simons a montré des talents exceptionnels dès son jeune âge. Diplômé à l’âge de vingt ans du MIT en mathématiques et littérature, il obtient par la suite un doctorat à Berkeley en 1962. Avant même de terminer son doctorat, il a été nommé professeur de mathématiques à l’Université de Lancaster et est devenu l’un des principaux cryptographes et codeurs de l’Institut d’analyse de la défense, où il a travaillé entre 1964 et 1968 jusqu’à ce qu’il démissionne en raison d’opinions divergents sur la guerre du Vietnam.
De retour dans le monde universitaire, il est nommé à l’âge de trente ans doyen du Département de mathématiques de l’Université de Stony Brook. Preuve de ses compétences, il remporte en 1976 le prix Oswald Veblen pour un travail dans le domaine de la géométrie qui a permis de démontrer la validité de la conjecture de Bernstein jusqu’à la huitième dimension. Cependant, en 1978, au milieu de son activité académique, Simons décide de quitter le monde universitaire pour se consacrer à la création d’un fonds d’investissement essentiellement basé sur l’utilisation des mathématiques financières. C’est ainsi qu’en 1982 Renaissance Technologies est née.
Stratégie de Renaissance
Le fonds utilise un trading systématique basé sur des modèles mathématiques complexes. Les modèles utilisés sont encore un mystère et font l’objet de nombreuses spéculations. D’après les déclarations de Simons, il apparaît que le fonds est basé sur des systèmes informatiques qui analysent toutes les données pouvant être collectées, même de nature non financière, à la recherche de mouvements non aléatoires et de schémas possibles.
Pour cette raison, l’une des particularités du fonds réside dans le fait que la majorité des salariés ont une formation non financière. En effet, plus de 90% des salariés ont des qualifications scientifiques, titulaires d’un doctorat en informatique, mathématiques, physique, astrophysique et statistiques. Le PDG, Peter Brown, est lui-même mathématicien titulaire d’un doctorat en informatique, comme presque tous les personnages clés du fonds.
Les premiers collaborateurs de Simons étaient des informaticiens travaillant sur le programme d’intelligence artificielle d’IBM et ont contribué au développement du premier algorithme. Grâce à l’apprentissage automatique, Renaissance a développé des algorithmes capables de prédire les changements de prix et de faire des prévisions précises à travers des séries chronologiques.
Le succès du fonds dépend aussi du turnover quasi nul : grâce aux primes et incitations accordées aux salariés, très peu d’entre eux quittent leur emploi. C’est une raison qui explique pourquoi les secrets de son algorithme n’ont pas encore été dévoilés. Les rares déclarations des cadres et l’emplacement isolé hautement protégé par des systèmes de sécurité contribuent également au maintien du secret, alimentant la légende et la spéculation sur la stratégie fonds.
Beaucoup pensent que le fonds a développé un modèle avec de nombreuses composantes déterministes, dans lequel les composantes stochastiques et aléatoires n’apparaissent que de manière résiduelle. Si c’est vrai, ce modèle serait la “pierre philosophale” des fonds spéculatifs.